The model assumes an underlying Poisson point pattern and a Gaussian response, with intensity $\lambda$ of species 1 and 2 given by:
$\lambda_1 = peak_1 \times exp^{(-1/2 \times \dfrac{(temp - \mu_1)^2}{\sigma_1^2} + e_1)}$
$\lambda_2 = peak_2 \times exp^{(-1/2 \times \dfrac{(temp - \mu_2)^2}{\sigma_2^2} + e_2)}$
where $temp$ is the predictor, $\mu_1$ and $\mu_2$ are the niche mean for each species, and $\sigma_1$ and $\sigma_2$ represent the niche breath. The variables $peak_1$ and $peak_2$ are constants to that set the expected abundance at the mean.
Both species are associated through a residuals $e_1$ and $e_2$:
$e_{ij} \sim \textsf{MVN}(0, \Sigma)$
Residuals have a multivariate (bivariate) normal distribution with mean zero and covariance matrix,
$\Sigma = \begin{bmatrix} var_{1,1} & cov_{1,2} \\ cov_{2,1} & var_{2,2} \end{bmatrix}$
The inverse of the covariance matrix is called the precision matrix, denoted by $\tau = {\Sigma}^{-1}$.
Function
The function two2tango() needs the following arguments:
mu_1= $\mu_1$ andmu_2= $\mu_2$: the mean of the response curve (niche mean) for each species,sigma_1= $\sigma_1$ andsigma_2= $\sigma_2$: the SD of the response curve (niche breath) for each species,peak_1= $peak_1$ andpeak_2= $peak_2$: constants that set the expected abundance at the mean,var= $var_{1,1}$ = $var_{2,2}$: the variance of each species, which will always be set to1,cov1= $cov_{1,2}$ and $cov_{2,1}$: the covariance of one species against the other, which needs to be symmetric.
Then it returns a list with two sf objects of POINT geometry, one
for each species.
library(spatstat)
library(tmap)
tmap_mode("plot")
library(terra)
library(gstat)
library(sf)
library(tidyverse)
# functions
source('code/two2tango.R')
source('code/auxiliary.R')
Test the function
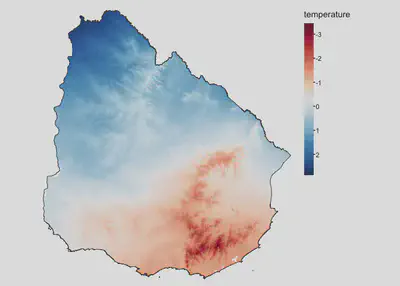
We will use as an example covariate the average annual temperature for Uruguay
uruguay <- geodata::gadm(country = 'UY', level=0, path = 'data/')
temperature <- geodata::worldclim_country('UY', var = 'tavg', path = 'data/')
temperature <- mean(temperature, na.rm=T) %>% mask(uruguay)
temp <- scale(temperature)
tm_shape(temp) +
tm_raster(col.scale = tm_scale_continuous(midpoint = NA, values = 'brewer.rd_bu'),
col.legend = tm_legend('temperature')) +
tm_shape(uruguay) +
tm_borders() +
tm_layout(frame=F, legend.frame = F)
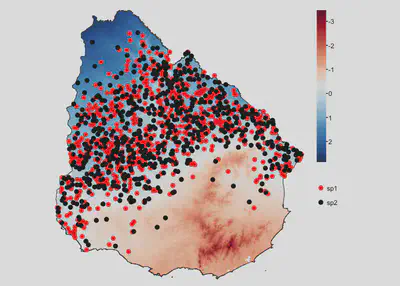
Case 1
Species have the same niche and co-occur
| $\mu_1$ | $\sigma_1$ | $peak_1$ | $var$ | $cov$ | |
|---|---|---|---|---|---|
sp1 | 0.5 | 0.5 | 60 | 1 | 0.9 |
sp2 | 0.5 | 0.5 | 60 | 1 | 0.9 |
mu1 = 0.5
mu2 = 0.5
sigma1 = 0.5
sigma2 = 0.5
peak1 = 60
peak2 = 60
cov= 0.9
simulated_species <- two2tango(peak1=peak1, peak2=peak2,
mu1=mu1, sigma1=sigma1,
mu2=mu2, sigma2=sigma2,
cov=cov,
predictor = temp)
sp1 <- simulated_species[[1]] %>% mutate(species = 'sp1')
sp2 <- simulated_species[[2]] %>% mutate(species = 'sp2')
Code
tm_shape(temp) +
tm_raster(col.scale = tm_scale_continuous(midpoint = NA, values = 'brewer.rd_bu'),
col.legend = tm_legend('')) +
tm_shape(uruguay) + tm_borders() +
tm_shape(sp1) +
tm_dots(fill='species',
fill.scale = tm_scale_categorical(values='red'),
fill.legend = tm_legend(''), size = 0.5) +
tm_shape(sp2) +
tm_dots(fill='species',
fill.scale = tm_scale_categorical(values='black'),
fill.legend = tm_legend(''), size = 0.5) +
tm_layout(frame=F, legend.frame = F)
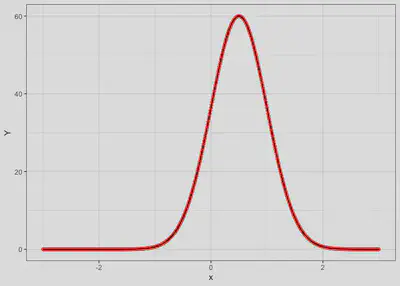
Code
response.df <- tibble(x = seq(-3, 3, by = 0.01),
y1 = spec.response(x, mu1, peak1, sigma1),
y2 = spec.response(x, mu2, peak2, sigma2))
ggplot() +
geom_line(data=response.df, aes(x=x, y=y1), col='red', linetype = 'dashed') +
geom_point(data=response.df, aes(x=x, y=y1), col='red') +
geom_line(data=response.df, aes(x=x, y=y2), col='black') +
geom_line(data=response.df, aes(x=x, y=y2), col='black') +
labs(y='Y') + theme_bw()
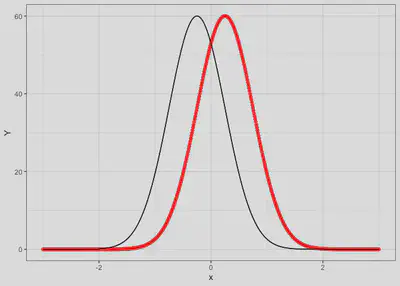
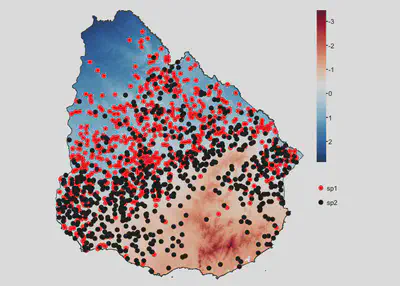
Case 2
Species have a different niche and negative co-occurrence
| $\mu_1$ | $\sigma_1$ | $peak_1$ | $var$ | $cov$ | |
|---|---|---|---|---|---|
sp1 | 0.25 | 0.5 | 60 | 1 | -0.9 |
sp2 | -0.25 | 0.5 | 60 | 1 | -0.9 |
mu1 = 0.25
mu2 = -0.25
sigma1 = 0.5
sigma2 = 0.5
peak1 = 60
peak2 = 60
cov= -0.9
simulated_species <- two2tango(peak1=peak1, peak2=peak2,
mu1=mu1, sigma1=sigma1,
mu2=mu2, sigma2=sigma2,
cov=cov,
predictor = temp)
sp1 <- simulated_species[[1]] %>% mutate(species = 'sp1')
sp2 <- simulated_species[[2]] %>% mutate(species = 'sp2')
Code
tm_shape(temp) +
tm_raster(col.scale = tm_scale_continuous(midpoint = NA, values = 'brewer.rd_bu'),
col.legend = tm_legend('')) +
tm_shape(uruguay) + tm_borders() +
tm_shape(sp1) +
tm_dots(fill='species',
fill.scale = tm_scale_categorical(values='red'),
fill.legend = tm_legend(''), size = 0.5) +
tm_shape(sp2) +
tm_dots(fill='species',
fill.scale = tm_scale_categorical(values='black'),
fill.legend = tm_legend(''), size = 0.5) +
tm_layout(frame=F, legend.frame = F)
Code
response.df <- tibble(x = seq(-3, 3, by = 0.01),
y1 = spec.response(x, mu1, peak1, sigma1),
y2 = spec.response(x, mu2, peak2, sigma2))
ggplot() +
geom_line(data=response.df, aes(x=x, y=y1), col='red', linetype = 'dashed') +
geom_point(data=response.df, aes(x=x, y=y1), col='red') +
geom_line(data=response.df, aes(x=x, y=y2), col='black') +
geom_line(data=response.df, aes(x=x, y=y2), col='black') +
labs(y='Y') + theme_bw()
Florencia Grattarola
Postdoc Researcher
Uruguayan biologist doing research in macroecology and biodiversity informatics.